RECOMBINATION CALCULATOR
This calculator determines the effective lifetime and recombination rate in crystalline silicon. It calculates radiative recombination, Auger recombination, and Shockley–Read–Hall recombination as a function of the dopant concentration, excess carrier concentration, or the separation of quasi-Fermi levels (sometimes called the implied open-circuit voltage).
DISCLAIMER
Neither PV Lighthouse nor any person related to the compilation of this calculator make any warranty, expressed or implied, or assume any legal liability or responsibility for the accuracy, completeness or usefulness of any information disclosed or rendered by this calculator.
WARNING
Although temperature is an input, its effect is not included in every recombination model – see the table below.
In particular, be aware that (i) the SRH model assumes constant lifetimes (or capture cross sections) even though they actually
depend strongly on temperature; (ii) the only Auger model that contains
a temperature dependence is Altermatt1997 (valid for 70–400 K), and (iii) the various radiative
recombination models are valid over different temperature ranges.
Hence, be wary of the results for any recombination rate, lifetime, or diffusion length when the temperature
lies outside the range specified by the recombination models (see table below).
When sweeping temperature, only the results for temperature-dependent models are plotted.
EQUATIONS
The program first applies the band gap models to determine the effective intrinsic carrier concentration ni eff, the conduction band energy Ec, the valence band energy Ev, the electron Fermi energy EFn, and the hole Fermi energy EFp following the procedure used in the band gap calculator. The intrinsic Fermi energy Ei is defined to be zero.
The recombination rate is then calculated for radiative Urad, Auger UAug, and Shockley–Read–Hall USRH recombination mechanisms, which sum to give the total recombination rate:
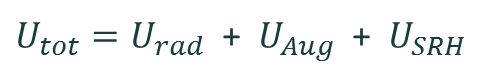
The lifetime for each mechanism is then determined by
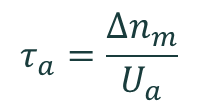
where Δnm is the excess minority carrier concentration, and where 'a' represents either 'rad', 'Aug' or 'SRH'. The effective lifetime τeff is calculated in the same way from Utot.
Various options are given for determining Urad and UAug, which all depend on the ionised dopant concentration ND+ or NA–, the excess electron Δn or hole Δp concentration, and ni eff. The options for the models are summarised in the table below.
The Shockley–Read–Hall recombination rate is calculated by the equation
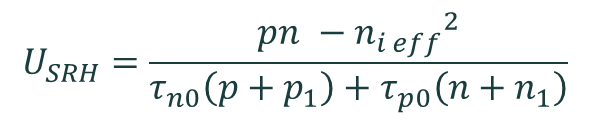
where

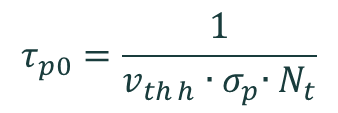
and
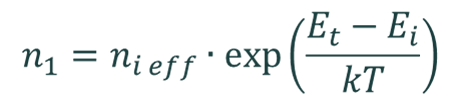
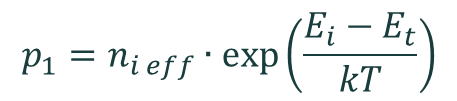
and where σn and σp are the capture cross sections of electrons and holes, vth e and vth h are the thermal velocities of electrons and holes, Nt is the concentration of defect states, and Et is the energy of the defect state. It is assumed that Nt << p, n, and that the semiconductor is not degenerate.
The calculator can also account for photon recycling. Photon recycling is when a fraction of the photons emitted via radiative recombination fpr are re-absorbed via band-to-band absorption before they exit the silicon. Thus, photon recycling effectively reduces radiative recombination. When photon recylcing is non-zero, the calculator gives the effective radiative recombinaion rate [Fel21],
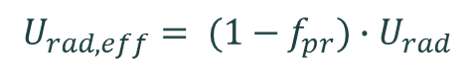
Models for fpr are given in the table below; they depend on the optical properties of the silicon wafer.
The electron diffusion length is determined from the equation Le = Sqrt(De⋅τ), where De is the diffusivity of electrons. An analogous equation is used to determine the hole diffusion length.
All equations also assume that the semiconductor is in steady state and that the steady state carrier concentrations relate to the equilibrium and excess carrier concentrations by n = n0 + Δn and p = p0 + Δp.
When selecting to plot the separation of quasi-Fermi levels on the x-axis of the figure, the program sweeps the excess carrier concentration, Δn = Δp, and plots the results against (EFn – EFp) / kT. This separation of quasi-Fermi levels is often referred to as the semiconductor's implied open-circuit voltage.
OPTIONS FOR RECOMBINATION MODELS



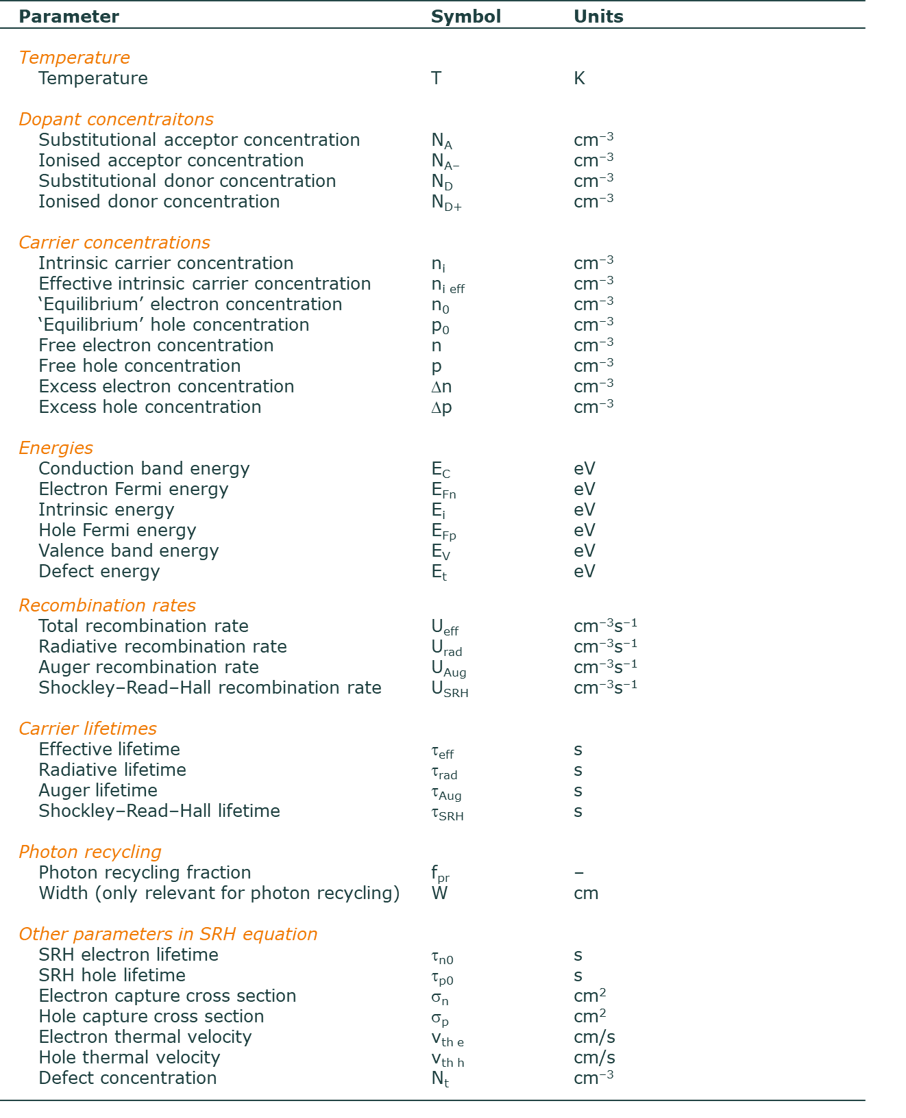
Definition of symbols
REFERENCES
| | |
| [Alt97] | P.P. Altermatt, J. Schmidt, G. Heiser and A.G. Aberle, "Assessment and parameterisation of Coulomb-enhanced Auger recombination coefficients in lowly injected crystalline silicon," Journal of Applied Physics 82, pp. 4938–4944, 1997. |
| [Alt05] | P.P. Altermatt, F. Geelhaar, T. Trupke, X. Dai, A. Neisser and E. Daub, "Injection dependence of spontaneous radiative recombination in c-Si: experiment, theoretical analysis, and simulation," Proc. 5th Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), pp. 47–48, 2005. |
| [Alt11] | P.P. Altermatt, "Models for numerical device simulations of crystalline silicon solar cells — a review," Journal of Computational Electronics 10 (3) pp. 314–330, 2011. |
| [Bla22] | L.E. Black and D.H. Macdonald, "On the quantification of Auger recombination in crystalline silicon," Solar Energy Materials and Solar Cells 234 111428, 2022. |
| [Dzi77] | J. Dziewior and W. Schmid, "Auger coefficients for highly doped and highly excited silicon," Applied Physics Letters 31, pp. 346–348, 1977. |
| [Fel21] | A. Fell, T. Niewelt, B. Steinhauser, F.D. Heinz, M.C. Schubert and S.W. Glunz, "Radiative recombination in silicon photovoltaics: Modeling the influence of charge carrier densities and photon recycling," Solar Energy Material and Solar Cells 230, 111198, 2021. |
| [Glu99] | S.W. Glunz, D. Biro, S. Rein and W. Warta, "Field-effect passivation of the SiO2–Si interfaceJournal of Applied Physics 86, pp. 683–691, 1999. |
| [Hal52] | R. Hall, "Electron–hole recombination in germanium," Physics Review 87, p. 387, 1952. |
| [Ker02] | M.J. Kerr and A. Cuevas, "General parameterization of Auger recombination in crystalline silicon," Journal of Applied Physics 91, pp. 2473–2480, 2002. |
| [Nie22] | T. Niewelt, B. Steinhauser, A. Richter, B. Veith-Wolf, A. Fell, B. Hammann, N.E. Grant, L. Black, J. Tan, A. Youssef, J.D. Murphy, J. Schmidt, M.C. Schubert and S.W. Glunz, "Reassessment of the intrinsic bulk recombination in crystalline silicon," Solar Energy Material and Solar Cells 235, 111467, 2022. |
| [Ngu14b] | H.T. Nguyen, S.C. Baker-Finch and D.H. Macdonald, "Temperature dependence of the radiative recombination coefficient in crystalline silicon from spectral photoluminescence," Applied Physics Letters 104, 112105, 2014. |
| [Ric12] | A. Richter, S.W. Glunz, F. Werner, J. Schmidt and A. Cuevas, "Improved quantitative description of Auger recombination in crystalline silicon," Physics Review B 86, 165202, 2012. |
| [Sch74] | H. Schlangenotto, H. Maeder and W. Gerlach, "Temperature dependence of the radiative recombination coefficient in silicon," Physica Status Solidi A 21, pp. 357–367, 1974. |
| [Sho52] | W. Shockley and W.T. Read, "Statistics of the recombinations of holes and electrons," Physics Review 87, pp. 835–842, 1952. |
| [Sin87] | R.A. Sinton and R.M. Swanson, "Recombination in highly injected silicon," IEEE Transactions on Electron Devices 34, pp. 1380–1389, 1987. |
| [Tru03] | T. Trupke, M.A. Green, P. Würfel, P.P. Altermatt, A. Wang, J. Zhao and R. Corkish, "Temperature dependence of the radiative recombination coefficient of intrinsic crystalline silicon," Journal of Applied Physics 94 (8), pp. 4930–4937, 2003. |
| [Vei18] | B.A. Veith–Wolf, S. Schäfer, R.Brendel and J.Schmidt, "Reassessment of intrinsic lifetime limit in n-type crystalline silicon and implication on maximum solar cell efficiency," Solar Energy Materials and Solar Cells 186, pp. 194–199, 2018. |
ACKNOWLEDGEMENTS AND FEEDBACK
We thank Tim Niewelt for sending us references models on updated models for Auger recombination, radiative recombination and photon recycling.
Please email corrections, comments or suggestions to support@pvlighthouse.com.au.