SHEET RESISTANCE CALCULATOR
This calculator determines the sheet resistance of an arbitrarily doped semiconductor at equilibrium (i.e., in the dark and with no applied voltage).
The calculator simulates a four-point probe measurement of a surface doped region, such as the emitter or the back-surface field of a photovoltaic solar cell. The user can either generate a dopant profile, or upload a profile from a SIMS, ECV, or spreading-resistance measurement. The calculator then determines the sheet resistance and the junction depth of the surface doped region at any temperature.
The sheet resistance ρsq at equilibrium is determined from the net ionised doping concentration N(z) and the mobility of the majority carriers μmaj by the equation
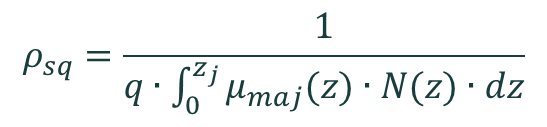
where zj is the junction depth and q is the charge of an electron. The sheet resistance has the dimensions Ω/sq.
The net ionised doping concentration is defined as N(z) = |NA(z) – ND(z)|, where NA and ND are the ionised concentration of acceptor and donor atoms. In the case of a silicon semiconductor, boron atoms are acceptors and phosphorus atoms are donors.
A doping profile can be uploaded from a CSV file or generated as an exponential, Gaussian, uniform or inverse error function (ERFC). The equations for these functions are shown below. The doping profile represents a surface diffusion, such as an emitter or a back-surface field. These are usually created by diffusing dopant atoms into the semiconductor at high temperatures, but can also be created by implanting dopant atoms at high energies. A background concentration can be included in the analysis, which is necessarily a uniform doping profile.
The junction depth zj is defined as follows: If there is no background, zj equals the depth at which the minimum permissible dopant concentration Nmin occurs, as defined on the ''Option'' page; if the background and dopant profile are of opposite types, zj is the depth at which |NA(z) – ND(z)| equals zero; and if the background and dopant profiles are of the same type, zj equals the background thickness. The latter two definitions were chosen so that the simulator returns the sheet resistance that would be measured by an ideal four-point probe measurement.
The user has the option of several mobility models, which are described on the About page of the Mobility Calculator.
Warning: The input profile is the ionised dopant profile. It should not include inactive dopant atoms, like interstitial atoms, or non-ionised substitutional atoms, which can occur when the dopant concentration is high or the temperature low.
EQUATIONS FOR THE DOPING PROFILE
Like PC1D, the user can select from four equations where all are defined by a peak concentration Np, the depth of the peak concentration zp, and a depth factor zf.
PC1D defines zf such that the Gaussian and ERFC equations have the simplest form.
| Uniform: |
N(z) = Np for z ≤ zp and N(z) = 0 for z > zp |
| Exponential: |
N(z) = Np ⋅ exp[–|z – zp| / zf] |
| Gaussian: |
N(z) = Np ⋅ exp[–(z – zp)2 / zf2 ] |
| ERFC: |
N(z) = Np ⋅ {1 – erf[ (z – zp) / zf ] } |
The traditional approach to employing Gaussian and ERFC equations is to set the standard deviation as the third input parameter. In this calculator, the user can select to define zf as the standard deviation, in which case the profiles are defined as follows.
| Uniform: |
N(z) = Np for z ≤ zp and N(z) = 0 for z > zp |
| Exponential: |
N(z) = Np ⋅ exp[–|z – zp| / zf] |
| Gaussian: |
N(z) = Np ⋅ exp{–[ (z – zp) / (zf ⋅ √2) ]2} / [zf ⋅ √(2π)] |
| ERFC: |
N(z) = Np ⋅ {1 – erf[ (z – zp) / (zf ⋅ √2) ] } |
The selection of either the PC1D definition or the traditional definition of zf is now available on the ''Calculator'' page. Given the widespread use of PC1D in the field of photovoltaics, the default definition of zf follows the PC1D definition.
ACTIVE DOPING LIMIT
A maximum limit to the electrically active dopant concentration can be assigned. This maximum limit can be used to represent the solid solubility limit of the dopant species at a particular process temperature.
A future update of this calculator will include the solid solubility models from the literature.
MOBILITY MODELS
For c-Si, the user may choose from the mobility models of Klaassen [1,2], Arora [3] or Dorkel and Leturcq [4].
For more information on the use of these models we suggest you visit either the Mobility Calculator or the Resistivity Calculator.
ACKNOWLEDGEMENTS
We thank Fa-Jun Ma (SERIS) for finding a bug that caused an underestimation of the sheet resistance for B diffusions in versions preceding 1.4 (12-Apr-2013); and Kean Fong (ANU) for finding a bug that caused an overestimation of the sheet resistance for ''traditional'' Gaussian profiles in versions preceding 1.6 (4-Dec-2013). We also thank Dongchul Suh (ANU) and Yimao Wan (ANU), for the Korean and Chinese translations.
REFERENCES
| | |
| [1] | D.B.M. Klaassen, "A unified mobility model for device simulation—I. Model equations and concentration dependence," Solid-State Electronics, 35 (7), pp. 953–959, 1992. |
| [2] | D.B.M. Klaassen, "A unified mobility model for device simulation—II. Temperature dependence of carrier mobility and lifetime," Solid-State Electronics, 35 (7), pp. 961–967, 1992. |
| [3] | N.D. Arora, J.R. Hauser and D.J. Roulston, "Electron and hole mobilities in silicon as a function of concentration and temperature," IEEE Transactions on Electron Devicies, ED-29 (2), pp. 292–295, 1982. |
| [4] | J.M. Dorkel and PH. Leturcq, "Carrier mobilities in silicon semi-empirically related to temperature, doping and injection level," Solid-State Electronics, 24 (9), pp. 821–825, 1981. |
FEEDBACK
Please email corrections, comments or suggestions to support@pvlighthouse.com.au.