It determines the concentration of various impurities as a function of position within a silicon ingot. The resulting resistivity and carrier lifetime are also calculated.

Based on the physical model described by Coletti [Col11], this calculator allows the user to compare the Coletti model to their experimental results.

The ingot impurity calculator was conceived by Gianluca Coletti (ECN). The calculator was created by Gianluca and PV Lighthouse.

The user inserts the initial concentration C₀ of various impurities within the molten silicon that is used to form the ingot, as well as the effective segregation coefficient k_eff for each impurity. The calculator then determines the impurity concentration as a function of position in the silicon ingot via the normal freezing equation,

,

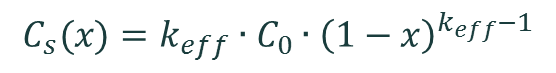where x is the normalised distance from the bottom of the ingot (i.e., 0 ≤ x ≤ 1).

The calculator next computes the active concentration of defects that are induced in the silicon by the impurities,

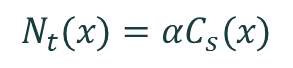
where a is the electrical activity, or more specifically, the fraction of impurity atoms that introduce a defect state at an energy within the 'forbidden gap' of the silicon in the final solar cell. The electrical activity is influenced by phenomena like precipitation, gettering, and hydrogenation. Its value therefore depends on the elemental species and on the process used to fabricate the solar cell. It is assumed here that a is constant with position within the ingot although this is not necessarily true. The definition of a is given in [Col11].

The calculator allows the user to dope the silicon with boron (B) and phosphorus (P) using the same procedure. Consequently, the net doping in the ingot varies with x (unless k_eff = 1). Note that for B and P, the ionised fraction of N_t(x) depends on the ionisation model selected under 'physical models'; for other impurities, the ionisation fraction is assumed to be 100%.

The resistivity of the siicon is calculated from the concentrations of B and P. It neglects the contribution from other impurities. Note that the resistivity depends on the excess carrier concentration Δn; therefore, set Δn = 0 cm⁻³ to determine the equilibrium resistivity (i.e., the resistivity of the silicon in the dark).

With the dopant and impurity concentrations—as well as inputs for the nine physical models that describe the silicon's semiconductor properties—the calculator determines the carrier lifetime for a given excess carrier concentration ∆n. This requires the user to insert the defect energy level E_t relative to the intrinsic energy level E_i, and the capture cross sections of electrons σ_n and holes σ_p, for each defect state. The calculations do not account for carrier trapping, and therefore the excess electron concentration equals the excess hole concentration (∆n = ∆p).

Note that for some impurities, a can be selected from a dropdown list with reference to a particular publication (e.g., [Col11]). In such cases, a was determined for a specific set of processing conditions and for specific values of E_t – E_i, σ_n and σ_p. For consistency, use the same input values that were used in the publication to calculate carrier lifetimes.

The calculations for the recombination and semiconductor properties are explained on the 'about' tabs of the recombination calculator and the band gap calculator. For now, the temperature is limited to 300 K.

The procedure and the relevance of the ingot impurity calculator is further described in [Col11], [Col13] and [Dav80].

Neither PV Lighthouse nor any person related to the compilation of this calculator make any warranty, expressed or implied, or assume any legal liability or responsibility for the accuracy, completeness or usefulness of any information disclosed or rendered by this calculator.

[Col08]	Reference not found
[Col11]	Reference not found
[Col13]	Reference not found
[Dav80]	Reference not found
[Ist99]	Reference not found
[Pau09]	Reference not found
[Pau10]	Reference not found
[Sch07]	Reference not found

Please email corrections, comments or suggestions to support@pvlighthouse.com.au.